Get started with `{epipredict}`

Introduction

At a high level, the goal of epipredict is to make it easy to run simple machine learning and statistical forecasters for epidemiological data. To do this, we have extended the tidymodels framework to handle the case of panel time-series data.

Our hope is that it is easy for users with epidemiological training and some statistical knowledge to fit baseline models, while also allowing those with more nuanced statistical understanding to create complex custom models using the same framework. Towards that end, epipredict provides two main classes of tools:

Canned forecasters

A set of basic, easy-to-use “canned” forecasters that work out of the box. We currently provide the following basic forecasters:

Flatline forecaster: predicts as the median the most recently seen value with increasingly wide quantiles.
Climatological forecaster: predicts the median and quantiles based on the historical values around the same date in previous years.
Autoregressive forecaster: fits a model (e.g. linear regression) on lagged data to predict quantiles for continuous values.
Autoregressive classifier: fits a model (e.g. logistic regression) on lagged data to predict a binned version of the growth rate.
CDC FluSight flatline forecaster: a variant of the flatline forecaster that is used as a baseline in the CDC’s FluSight forecasting competition.

Forecasting framework

A framework for creating custom forecasters out of modular components, from which the canned forecasters were created. There are three types of components:

Preprocessor: transform the data before model training, such as converting counts to rates, creating smoothed columns, or any {recipes} step
Trainer: train a model on data, resulting in a fitted model object. Examples include linear regression, quantile regression, or any {parsnip} engine.
Postprocessor: unique to epipredict; used to transform the predictions after the model has been fit, such as
- generating quantiles from purely point-prediction models,
- reverting operations done in the steps, such as converting from rates back to counts
- generally adapting the format of the prediction to its eventual use.

The rest of this “Get Started” vignette will focus on using and modifying the canned forecasters. Check out the Custom Epiworkflows vignette for examples of using the forecaster framework to make more complex, custom forecasters.

If you are interested in time series in a non-panel data context, you may also want to look at timetk and modeltime for some related techniques.

For a more in-depth treatment with some practical applications, see also the Forecasting Book.

Panel forecasting basics

Example data

The forecasting methods in this package are designed to work with panel time series data in epi_df format as made available in the epiprocess package. An epi_df is a collection of one or more time-series indexed by one or more categorical variables. The {epidatasets} package makes several pre-compiled example datasets available. Let’s look at an example epi_df:

covid_case_death_rates
#> An `epi_df` object, 20,496 x 4 with metadata:
#> * geo_type  = state
#> * time_type = day
#> * as_of     = 2023-03-10
#> 
#> # A tibble: 20,496 × 4
#>   geo_value time_value case_rate death_rate
#> * <chr>     <date>         <dbl>      <dbl>
#> 1 ak        2020-12-31      35.9      0.158
#> 2 al        2020-12-31      65.1      0.438
#> 3 ar        2020-12-31      66.0      1.27 
#> 4 as        2020-12-31       0        0    
#> 5 az        2020-12-31      76.8      1.10 
#> 6 ca        2020-12-31      95.9      0.755
#> # ℹ 20,490 more rows

This dataset uses a single key, geo_value, and two separate time series, case_rate and death_rate. The keys are represented in “long” format, with separate columns for the key and the value, while separate time series are represented in “wide” format with each time series stored in a separate column.

epiprocess is designed to handle data that always has a geographic key, and potentially other key values, such as age, ethnicity, or other demographic information. For example, grad_employ_subset from epidatasets also has both age_group and edu_qual as additional keys:

grad_employ_subset
#> An `epi_df` object, 1,445 x 7 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = age_group, edu_qual
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 1,445 × 7
#>   geo_value           age_group      edu_qual        time_value num_graduates
#> * <chr>               <fct>          <fct>                <int>         <dbl>
#> 1 Newfoundland and L… 15 to 34 years Career, techni…       2010           430
#> 2 Newfoundland and L… 35 to 64 years Career, techni…       2010           140
#> 3 Newfoundland and L… 15 to 34 years Career, techni…       2010           630
#> 4 Newfoundland and L… 35 to 64 years Career, techni…       2010           140
#> 5 Newfoundland and L… 15 to 34 years Other career, …       2010            60
#> 6 Newfoundland and L… 35 to 64 years Other career, …       2010            40
#> # ℹ 1,439 more rows
#> # ℹ 2 more variables: med_income_2y <dbl>, med_income_5y <dbl>

See epiprocess for more details on the epi_df format.

Panel time series are ubiquitous in epidemiology, but are also common in economics, psychology, sociology, and many other areas. While this package was designed with epidemiology in mind, many of the techniques are more broadly applicable.

Customizing `arx_forecaster()`

Let’s expand on the basic example presented on the landing page, starting with adjusting some parameters in arx_forecaster().

The trainer argument allows us to set the fitting engine. We can use either one of the included engines, such as quantile_reg(), or one of the relevant parsnip models:

two_week_ahead <- arx_forecaster(
  covid_case_death_rates |> filter(time_value <= forecast_date),
  outcome = "death_rate",
  trainer = quantile_reg(),
  predictors = c("death_rate"),
  args_list = arx_args_list(
    lags = list(c(0, 7, 14)),
    ahead = 14
  )
)
hardhat::extract_fit_engine(two_week_ahead$epi_workflow)
#> Call:
#> quantreg::rq(formula = ..y ~ ., tau = ~c(0.05, 0.1, 0.25, 0.5, 
#> 0.75, 0.9, 0.95), data = data, na.action = stats::na.omit, method = ~"br", 
#>     model = FALSE)
#> 
#> Coefficients:
#>                      tau= 0.05  tau= 0.10 tau= 0.25  tau= 0.50  tau= 0.75
#> (Intercept)       -0.004873168 0.00000000 0.0000000 0.01867752 0.03708118
#> lag_0_death_rate   0.084091001 0.15180503 0.3076742 0.51165423 0.59058733
#> lag_7_death_rate   0.049478502 0.08493916 0.1232253 0.10018481 0.18480536
#> lag_14_death_rate  0.072304151 0.08554334 0.0712085 0.04088075 0.02609046
#>                    tau= 0.90 tau= 0.95
#> (Intercept)       0.07234641 0.1092061
#> lag_0_death_rate  0.59001978 0.5249616
#> lag_7_death_rate  0.33236190 0.4250353
#> lag_14_death_rate 0.03695928 0.1783820
#> 
#> Degrees of freedom: 10416 total; 10412 residual

The default trainer is parsnip::linear_reg(), which generates quantiles after the fact in the post-processing layers, rather than as part of the model. While this does work, it is generally preferable to use quantile_reg(), as the quantiles generated in post-processing can be poorly behaved. quantile_reg() on the other hand directly estimates a different linear model for each quantile, reflected in the several different columns for tau above.

Because of the flexibility of parsnip, there are a whole host of models available to us¹; as an example, we could have just as easily substituted a non-linear random forest model from ranger:

two_week_ahead <- arx_forecaster(
  covid_case_death_rates |> filter(time_value <= forecast_date),
  outcome = "death_rate",
  trainer = rand_forest(mode = "regression"),
  predictors = c("death_rate"),
  args_list = arx_args_list(
    lags = list(c(0, 7, 14)),
    ahead = 14
  )
)

Any other customization is routed through arx_args_list(); for example, if we wanted to increase the number of quantiles fit:

two_week_ahead <- arx_forecaster(
  covid_case_death_rates |>
    filter(time_value <= forecast_date, geo_value %in% used_locations),
  outcome = "death_rate",
  trainer = quantile_reg(),
  predictors = c("death_rate"),
  args_list = arx_args_list(
    lags = list(c(0, 7, 14)),
    ahead = 14,
    ############ changing quantile_levels ############
    quantile_levels = c(0.05, 0.1, 0.2, 0.3, 0.5, 0.7, 0.8, 0.9, 0.95)
    ##################################################
  )
)
hardhat::extract_fit_engine(two_week_ahead$epi_workflow)
#> Call:
#> quantreg::rq(formula = ..y ~ ., tau = ~c(0.05, 0.1, 0.2, 0.3, 
#> 0.5, 0.7, 0.8, 0.9, 0.95), data = data, na.action = stats::na.omit, 
#>     method = ~"br", model = FALSE)
#> 
#> Coefficients:
#>                     tau= 0.05    tau= 0.10    tau= 0.20     tau= 0.30
#> (Intercept)       -0.01329758 -0.006999475 -0.003226356  0.0001366959
#> lag_0_death_rate   0.25217750  0.257695857  0.486159095  0.6986147165
#> lag_7_death_rate   0.17210286  0.212294203  0.114016289  0.0704290267
#> lag_14_death_rate  0.08880828  0.057022770  0.013800329 -0.0654254593
#>                      tau= 0.50    tau= 0.70    tau= 0.80   tau= 0.90
#> (Intercept)        0.004395352  0.008467922  0.005495554  0.01626215
#> lag_0_death_rate   0.751695727  0.767243828  0.743676651  0.60494554
#> lag_7_death_rate   0.208846644  0.347907095  0.460814061  0.61021640
#> lag_14_death_rate -0.164693162 -0.234886556 -0.236950849 -0.20670731
#>                     tau= 0.95
#> (Intercept)        0.03468154
#> lag_0_death_rate   0.59202848
#> lag_7_death_rate   0.64532803
#> lag_14_death_rate -0.18566431
#> 
#> Degrees of freedom: 744 total; 740 residual

See the function documentation for arx_args_list() for more examples of the modifications available. If you want to make further modifications, you will need a custom workflow; see the Custom Epiworkflows vignette for details.

Generating multiple aheads

Frequently, one doesn’t want just a forecast for a single day, but a trajectory of forecasts for several weeks. We can do this with arx_forecaster() by looping over aheads; for example, to predict every day over a 4-week time period:

all_canned_results <- lapply(
  seq(0, 28),
  \(days_ahead) {
    arx_forecaster(
      covid_case_death_rates |>
        filter(time_value <= forecast_date, geo_value %in% used_locations),
      outcome = "death_rate",
      predictors = c("case_rate", "death_rate"),
      trainer = quantile_reg(),
      args_list = arx_args_list(
        lags = list(c(0, 1, 2, 3, 7, 14), c(0, 7, 14)),
        ahead = days_ahead
      )
    )
  }
)
# pull out the workflow and the predictions to be able to
#  effectively use autoplot
workflow <- all_canned_results[[1]]$epi_workflow
results <- purrr::map_df(all_canned_results, ~ `$`(., "predictions"))
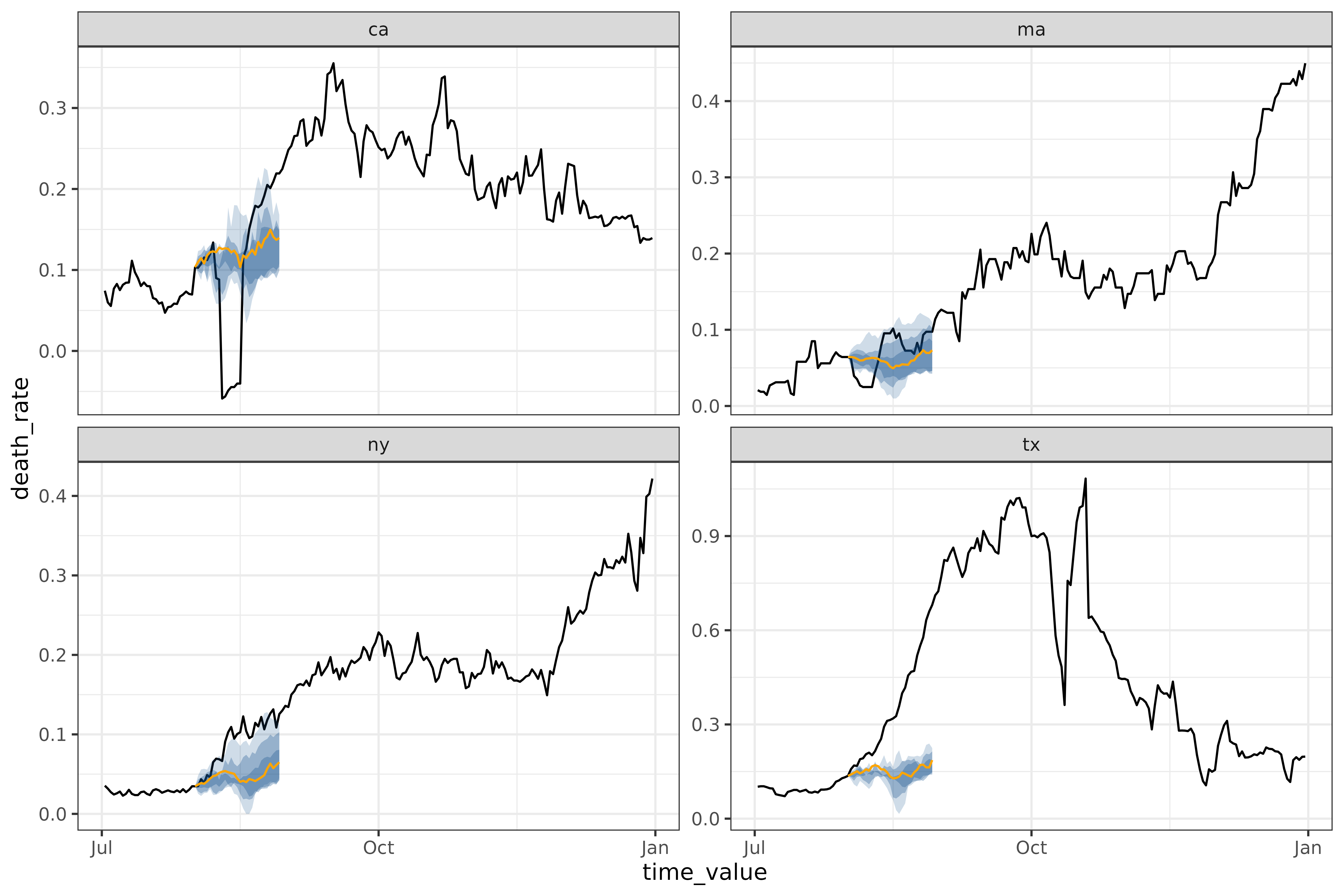
autoplot(
  object = workflow,
  predictions = results,
  plot_data = covid_case_death_rates |>
    filter(geo_value %in% used_locations, time_value > "2021-07-01")
)

Other canned forecasters

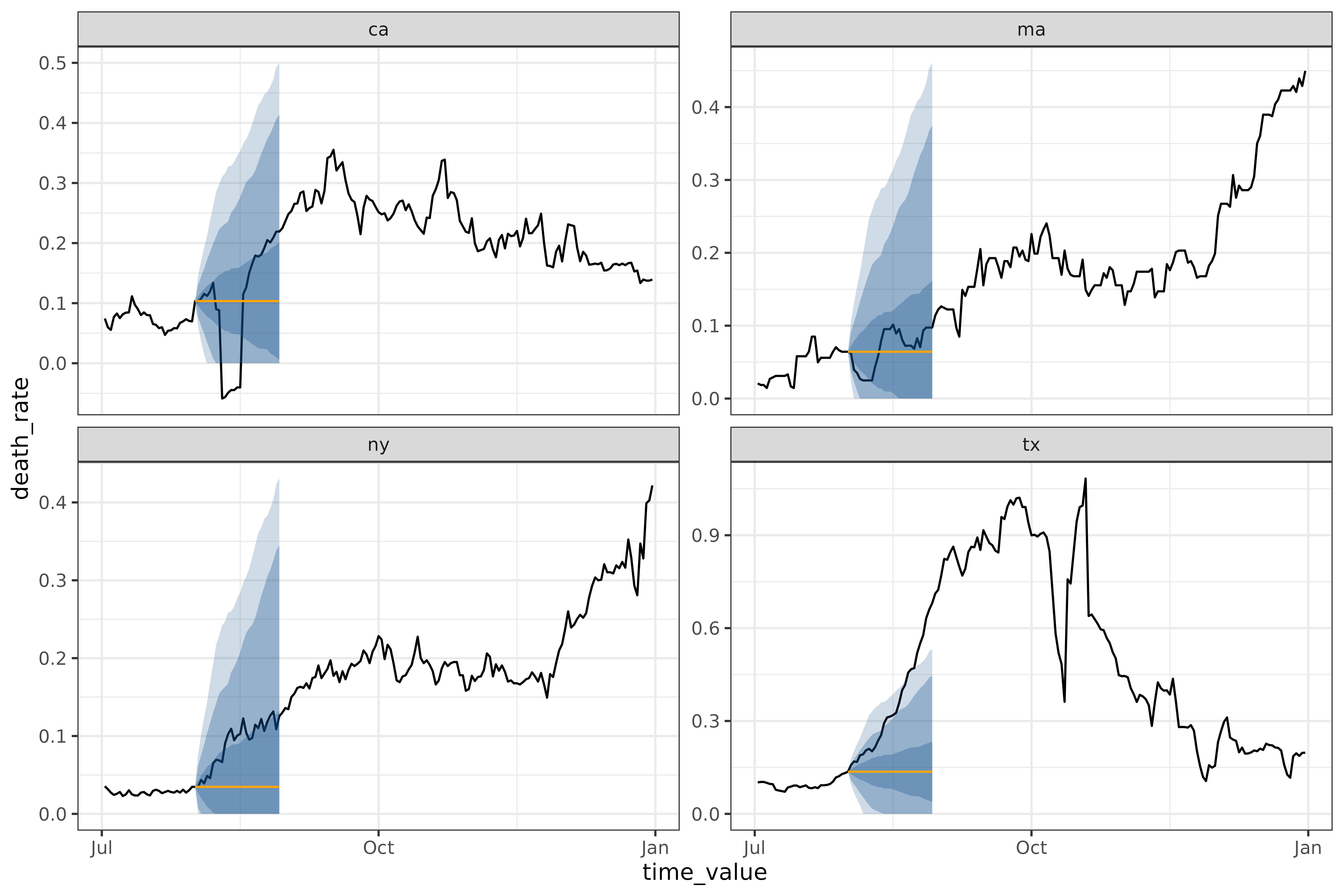
`flatline_forecaster()`

The simplest model we provide is the flatline_forecaster(), which predicts a flat line (with quantiles generated from the residuals using layer_residual_quantiles()). For example, on the same dataset as above:

all_flatlines <- lapply(
  seq(0, 28),
  \(days_ahead) {
    flatline_forecaster(
      covid_case_death_rates |>
        filter(time_value <= forecast_date, geo_value %in% used_locations),
      outcome = "death_rate",
      args_list = flatline_args_list(
        ahead = days_ahead,
      )
    )
  }
)
# same plotting code as in the arx multi-ahead case
workflow <- all_flatlines[[1]]$epi_workflow
results <- purrr::map_df(all_flatlines, ~ `$`(., "predictions"))
autoplot(
  object = workflow,
  predictions = results,
  plot_data = covid_case_death_rates |> filter(geo_value %in% used_locations, time_value > "2021-07-01")
)

`cdc_baseline_forecaster()`

This is a different method of generating a flatline forecast, used as a baseline for COVID19ForecastHub.

all_cdc_flatline <- 
cdc_baseline_forecaster(
  covid_case_death_rates |>
    filter(time_value <= forecast_date, geo_value %in% used_locations),
  outcome = "death_rate",
  args_list = cdc_baseline_args_list(
    aheads = 1:28,
    data_frequency = "1 day"
  )
)
# same plotting code as in the arx multi-ahead case
workflow <- all_cdc_flatline$epi_workflow
results <- all_cdc_flatline$predictions
autoplot(
  object = workflow,
  predictions = results,
  plot_data = covid_case_death_rates |> filter(geo_value %in% used_locations, time_value > "2021-07-01")
)

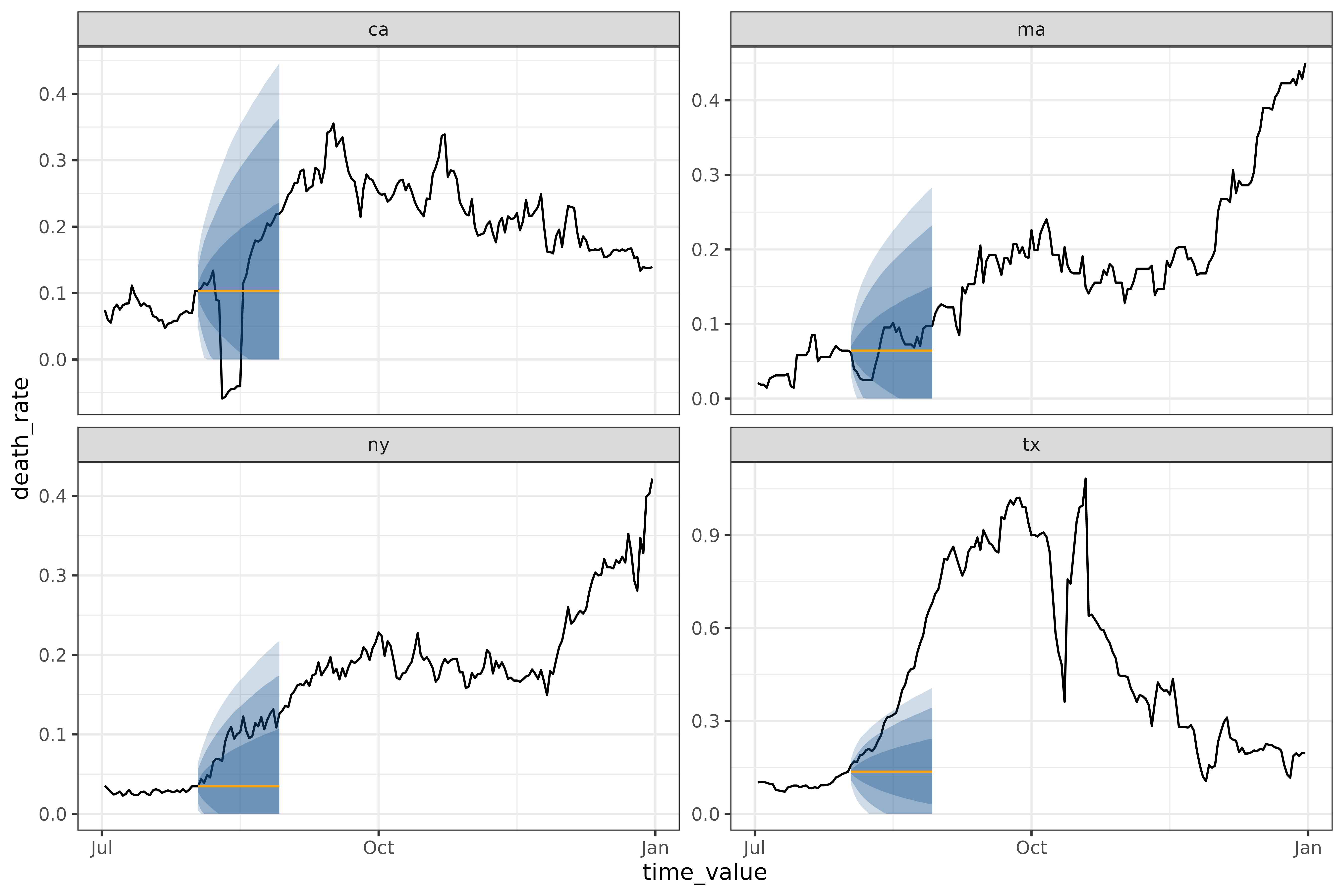
The median is the same, but the quantiles are generated using layer_cdc_flatline_quantiles() instead of layer_residual_quantiles(). Both rely on the computing the quantiles of the residuals, but this model extrapolates the quantiles by repeatedly sampling the initial quantiles to generate the next quantiles. This results in much smoother quantiles, but ones that only capture the one-ahead uncertainty.

`climatological_forecaster()`

A different kind of baseline, the climatological_forecaster() forecasts the point forecast and quantiles based on the historical values for this time of year, rather than extrapolating from recent values. For example, on the same dataset as above:

all_climate <- climatological_forecaster(
  covid_case_death_rates_extended |>
    filter(time_value <= forecast_date, geo_value %in% used_locations),
  outcome = "death_rate",
  args_list = climate_args_list(
    forecast_horizon = seq(0, 28),
    window_size = 14,
    time_type = "day",
    forecast_date = forecast_date
  )
)
workflow <- all_climate$epi_workflow
results <- all_climate$predictions
autoplot(
  object = workflow,
  predictions = results,
  plot_data = covid_case_death_rates_extended |> filter(geo_value %in% used_locations, time_value > "2021-07-01")
)

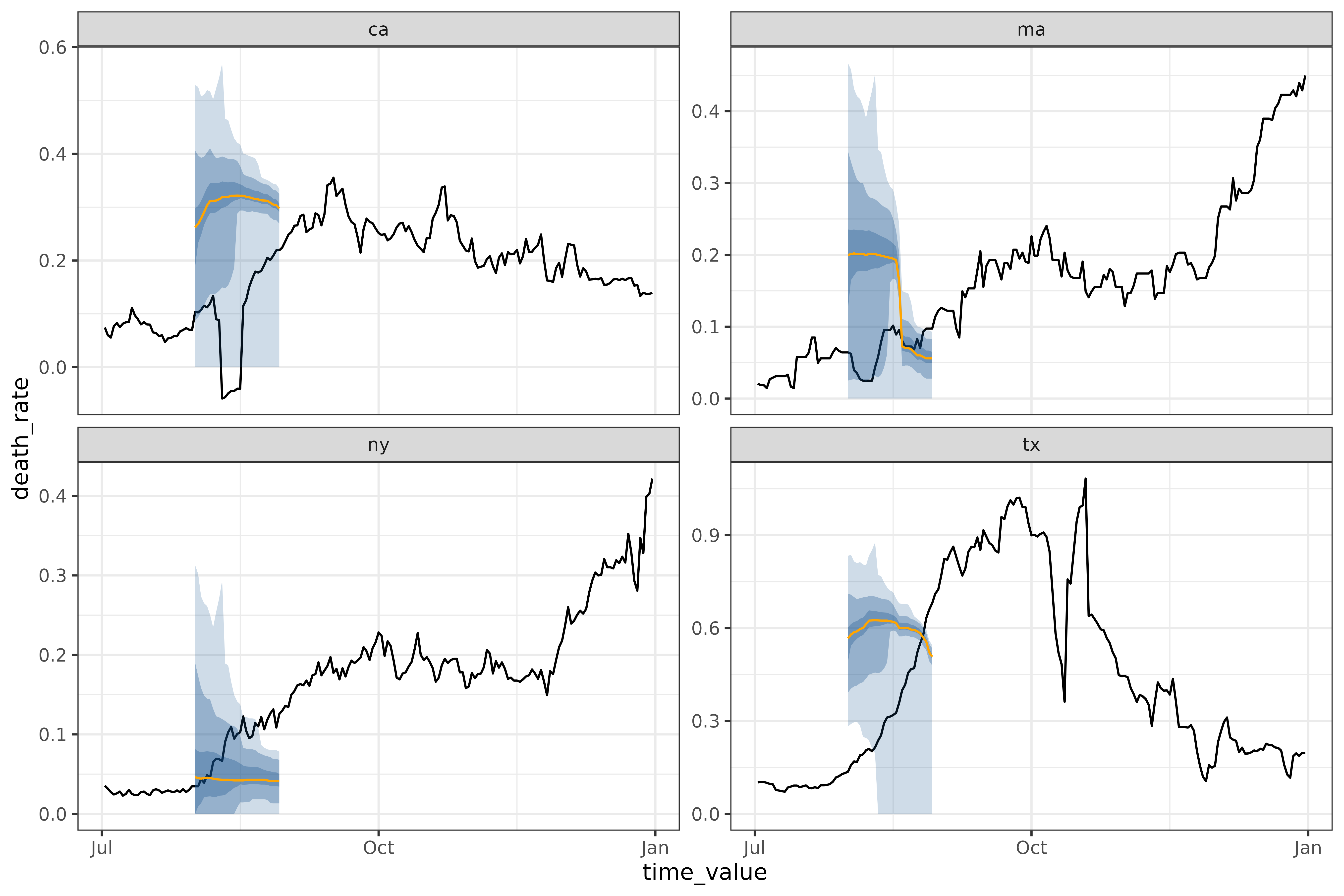
Note that we’re using covid_case_death_rates_extended rather than covid_case_death_rates, since it starts in March of 2020 rather than December. Without at least a year’s worth of historical data, it is impossible to do a climatological model. Even with only one year as we have here the resulting forecasts are unreliable.

One feature of the climatological baseline is that it forecasts multiple aheads simultaneously. This is possible for arx_forecaster(), but only using trainer = smooth_quantile_reg(), which is built to handle multiple aheads simultaneously.

`arx_classifier()`

The most complicated of the canned forecasters, arx_classifier first translates the outcome into a growth rate, and then classifies that growth rate into bins. For example, on the same dataset and forecast_date as above, we get:

classifier <- arx_classifier(
  covid_case_death_rates |>
    filter(geo_value %in% used_locations, time_value < forecast_date),
  outcome = "death_rate",
  predictors = c("death_rate", "case_rate"),
  trainer = multinom_reg(),
  args_list = arx_class_args_list(
    lags = list(c(0, 1, 2, 3, 7, 14), c(0, 7, 14)),
    ahead = 2 * 7,
    breaks = c(-0.01, 0.01, 0.1)
  )
)
classifier$predictions
#> # A tibble: 4 × 4
#>   geo_value .pred_class  forecast_date target_date
#>   <chr>     <fct>        <date>        <date>     
#> 1 ca        (-0.01,0.01] 2021-07-31    2021-08-14 
#> 2 ma        (-0.01,0.01] 2021-07-31    2021-08-14 
#> 3 ny        (-0.01,0.01] 2021-07-31    2021-08-14 
#> 4 tx        (-0.01,0.01] 2021-07-31    2021-08-14

The prediction splits into 4 cases: (-∞, -0.01), (-0.01, 0.01), (0.01, 0.1), and (0.1, ∞). In this case, the classifier put all 4 of the states in the same category, (0.01, 0.1). TODO effected by the old data. The number and size of the categories is controlled by breaks, which gives the boundary values.

For comparison, the growth rates for the target_date, as computed using epiprocess:

growth_rates <- covid_case_death_rates |>
  filter(geo_value %in% used_locations) |>
  group_by(geo_value) |>
  mutate(
    deaths_gr = growth_rate(x = time_value, y = death_rate)
  ) |>
  ungroup()
growth_rates |> filter(time_value == "2021-08-14")
#> An `epi_df` object, 4 x 5 with metadata:
#> * geo_type  = state
#> * time_type = day
#> * as_of     = 2023-03-10
#> 
#> # A tibble: 4 × 5
#>   geo_value time_value case_rate death_rate deaths_gr
#>   <chr>     <date>         <dbl>      <dbl>     <dbl>
#> 1 ca        2021-08-14      32.1    -0.0446   -1.39  
#> 2 ma        2021-08-14      16.8     0.0953    0.0633
#> 3 ny        2021-08-14      21.0     0.0946    0.0321
#> 4 tx        2021-08-14      48.4     0.311     0.0721

Unfortunately, this forecast was not particularly accurate, since for example -1.39 is not remotely in the interval (-0.01, 0.01].

Fitting multi-key panel data

If you have multiple keys that are set in the epi_df as other_keys, arx_forecaster will automatically group by those as well. For example, predicting the number of graduates in each of the categories in grad_employ from above:

# only fitting a subset, otherwise there are ~550 distinct pairs, which is bad for plotting
edu_quals <- c("Undergraduate degree", "Professional degree")
geo_values <- c("Quebec", "British Columbia")
grad_forecast <- arx_forecaster(
  grad_employ_subset |>
    filter(time_value < 2017) |>
    filter(edu_qual %in% edu_quals, geo_value %in% geo_values),
  outcome = "num_graduates",
  predictors = c("num_graduates"),
  args_list = arx_args_list(
    lags = list(c(0, 1, 2)),
    ahead = 1
  )
)
# and plotting
autoplot(
  grad_forecast$epi_workflow,
  grad_forecast$predictions,
  grad_employ_subset |>
    filter(edu_qual %in% edu_quals, geo_value %in% geo_values),
)

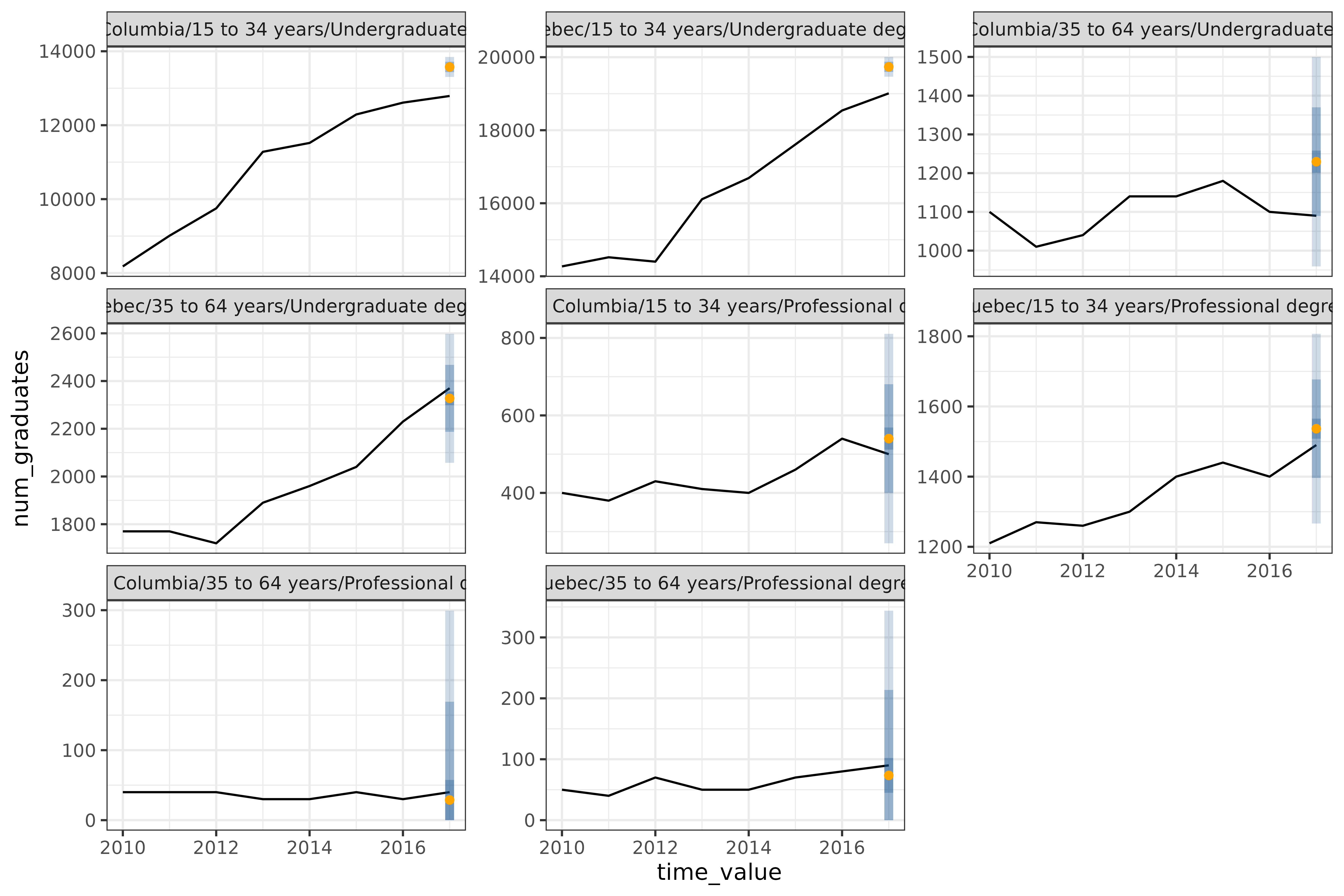
The 8 graphs are all pairs of the geo_values ("Quebec" and "British Columbia"), edu_quals ("Undergraduate degree" and "Professional degree"), and age brackets ("15 to 34 years" and "35 to 64 years").

Fitting a non-geo-pooled model

Because our internal methods fit a single model, to fit a non-geo-pooled model that has a different fit for each geography, one either needs a multi-level engine (which at the moment parsnip doesn’t support), or one needs to map over geographies.

geo_values <- covid_case_death_rates |>
  pull(geo_value) |>
  unique()

all_fits <-
  purrr::map(geo_values, \(geo) {
    covid_case_death_rates |>
      filter(
        geo_value == geo,
        time_value <= forecast_date
      ) |>
      arx_forecaster(
        outcome = "death_rate",
        trainer = linear_reg(),
        predictors = c("death_rate"),
        args_list = arx_args_list(
          lags = list(c(0, 7, 14)),
          ahead = 14
        )
      )
  })
map_df(all_fits, ~ pluck(., "predictions"))
#> # A tibble: 56 × 5
#>   geo_value  .pred .pred_distn forecast_date target_date
#>   <chr>      <dbl>   <qtls(7)> <date>        <date>     
#> 1 ak        0.0787    [0.0787] 2021-08-01    2021-08-15 
#> 2 al        0.206      [0.206] 2021-08-01    2021-08-15 
#> 3 ar        0.275      [0.275] 2021-08-01    2021-08-15 
#> 4 as        0              [0] 2021-08-01    2021-08-15 
#> 5 az        0.121      [0.121] 2021-08-01    2021-08-15 
#> 6 ca        0.0674    [0.0674] 2021-08-01    2021-08-15 
#> # ℹ 50 more rows

This is both 56 times slower², and uses far less data to fit each model. If the geographies are at all comparable, for example by normalization, we would get much better results by pooling.

If we wanted to build a geo-aware model, such as one that sets the constant in a linear regression fit to be different for each geography, we would need to build a Custom workflow with geography as a factor.

Anatomy of a canned forecaster

Code object

Let’s dissect the forecaster we trained back on the landing page:

four_week_ahead <- arx_forecaster(
  covid_case_death_rates |> filter(time_value <= forecast_date),
  outcome = "death_rate",
  predictors = c("case_rate", "death_rate"),
  args_list = arx_args_list(
    lags = list(c(0, 1, 2, 3, 7, 14), c(0, 7, 14)),
    ahead = 4 * 7,
    quantile_levels = c(0.1, 0.25, 0.5, 0.75, 0.9)
  )
)

four_week_ahead has two components: an epi_workflow, and a table of predictions. The table of predictions is simply a tibble of the predictions,

four_week_ahead$predictions
#> # A tibble: 56 × 5
#>   geo_value  .pred .pred_distn forecast_date target_date
#>   <chr>      <dbl>   <qtls(5)> <date>        <date>     
#> 1 ak        0.234      [0.234] 2021-08-01    2021-08-29 
#> 2 al        0.290       [0.29] 2021-08-01    2021-08-29 
#> 3 ar        0.482      [0.482] 2021-08-01    2021-08-29 
#> 4 as        0.0190     [0.019] 2021-08-01    2021-08-29 
#> 5 az        0.182      [0.182] 2021-08-01    2021-08-29 
#> 6 ca        0.178      [0.178] 2021-08-01    2021-08-29 
#> # ℹ 50 more rows

.pred gives the point/median prediction, while .pred_distn is a dist_quantiles() object representing a distribution through various quantile levels. The [6] in the name refers to the number of quantiles that have been explicitly created³; by default, this covers a 90% prediction interval, or 5% and 95%.

The epi_workflow is a significantly more complicated object, extending a workflows::workflow() to include post-processing:

four_week_ahead$epi_workflow
#> 
#> ══ Epi Workflow [trained] ═══════════════════════════════════════════════════
#> Preprocessor: Recipe
#> Model: linear_reg()
#> Postprocessor: Frosting
#> 
#> ── Preprocessor ─────────────────────────────────────────────────────────────
#> 
#> 6 Recipe steps.
#> 1. step_epi_lag()
#> 2. step_epi_lag()
#> 3. step_epi_ahead()
#> 4. step_naomit()
#> 5. step_naomit()
#> 6. step_training_window()
#> 
#> ── Model ────────────────────────────────────────────────────────────────────
#> 
#> Call:
#> stats::lm(formula = ..y ~ ., data = data)
#> 
#> Coefficients:
#>       (Intercept)    lag_0_case_rate    lag_1_case_rate    lag_2_case_rate  
#>         0.0190429          0.0022671         -0.0003564          0.0007037  
#>   lag_3_case_rate    lag_7_case_rate   lag_14_case_rate   lag_0_death_rate  
#>         0.0027288          0.0013392         -0.0002427          0.0926092  
#>  lag_7_death_rate  lag_14_death_rate  
#>         0.0640675          0.0347603
#> 
#> ── Postprocessor ────────────────────────────────────────────────────────────
#> 
#> 5 Frosting layers.
#> 1. layer_predict()
#> 2. layer_residual_quantiles()
#> 3. layer_add_forecast_date()
#> 4. layer_add_target_date()
#> 5. layer_threshold()
#>

An epi_workflow() consists of 3 parts:

Preprocessor: a collection of steps that transform the data to be ready for modelling. They come from this package or any of the recipes steps; four_week_ahead has 5 of these, and you can inspect them more closely by running hardhat::extract_recipe(four_week_ahead$epi_workflow).⁴
Model: the actual model that does the fitting, given by a parsnip::model_spec; four_week_ahead has the default of parsnip::linear_reg(), which is a wrapper from parsnip for stats::lm(). You can inspect the model more closely by running hardhat::extract_fit_recipe(four_week_ahead$epi_workflow).
Postprocessor: a collection of layers to be applied to the resulting forecast, internal to this package. four_week_ahead just so happens to have 5 of as these well. You can inspect the layers more closely by running epipredict::extract_layers(four_week_ahead$epi_workflow).

See the Custom Epiworkflows vignette for recreating and then extending four_week_ahead using the custom forecaster framework.

Mathematical description

Let’s describe in more detail the actual fit model for a more minimal version of four_week_ahead:

four_week_small <- arx_forecaster(
  covid_case_death_rates |> filter(time_value <= forecast_date),
  outcome = "death_rate",
  predictors = c("case_rate", "death_rate"),
  args_list = arx_args_list(
    lags = list(c(0, 7, 14), c(0, 7, 14)),
    ahead = 4 * 7,
    quantile_levels = c(0.1, 0.25, 0.5, 0.75, 0.9)
  )
)
hardhat::extract_fit_engine(four_week_small$epi_workflow)
#> 
#> Call:
#> stats::lm(formula = ..y ~ ., data = data)
#> 
#> Coefficients:
#>       (Intercept)    lag_0_case_rate    lag_7_case_rate   lag_14_case_rate  
#>         0.0186296          0.0041617          0.0026782         -0.0003569  
#>  lag_0_death_rate   lag_7_death_rate  lag_14_death_rate  
#>         0.0929132          0.0641027          0.0348096

If $d_t$ is the death rate on day $t$ and $c_t$ is the case rate, then the model we’re fitting is:

$d_{t+28} = a_0 + a_1 d_t + a_2 d_{t-7} + a_3 d_{t-14} + a_4 c_t + a_5 c_{t-7} + a_6 c_{t-14}.$

For example, $a_1$ is lag_0_death_rate above, with a value of 0.0929132, while $a_5$ is 0.0026782.

The training data for fitting this linear model is created by creating a series of columns shifted by the appropriate amount; this makes it so that each row without NA values is a training point to fit the coefficients $a_0,\ldots, a_6$ .